hyperboloïde

hyperboloïde

hyperboloïde [ ipɛrbɔlɔid ] adj. et n. m.
• 1765; de hyperbole et -oïde
♦ Didact.
1 ♦ Rare En forme d'hyperbole.
2 ♦ N. m. Math. Quadrique à centre dont les sections planes sont des hyperboles. Hyperboloïde de révolution.

● hyperboloïde nom masculin Quadrique à centre dont les asymptotes forment un cône réel. ● hyperboloïde (expressions) nom masculin Hyperboloïde de révolution, hyperboloïde engendré par la rotation d'une hyperbole autour d'un de ses axes de symétrie.

⇒HYPERBOLOÏDE, adj. et subst. masc.
GÉOMÉTRIE
I. — Emploi adj., inus. Qui ressemble à une hyperbole, qui se rapproche d'une hyperbole. Courbes hyperboloïdes (Ac. Compl. 1842).
II. — Subst. masc. Surface dont l'équation aux coordonnées cartésiennes est algébrique et du second degré, et dont les asymptotes forment un cône réel. Hyperboloïde à une nappe, à deux nappes. Construction d'ellipsoïdes dont chacun devait être remplacé dans certains cas par deux systèmes d'hyperboloïdes conjugués (CAUCHY, Œuvres, 1830, p. 135). Tout point S de l'espace est le sommet d'un cône réel circonscrit à l'hyperboloïde suivant une conique (E. BOREL, Paradoxes infini, 1946, p. 63).
♦ Hyperboloïde de révolution. ,,Surface engendrée par la révolution d'une hyperbole autour d'un de ses axes`` (Sc. 1962). Ainsi, dans le cas des miroirs, si la surface réfléchissante est un ellipsoïde ou un hyperboloïde (...) de révolution les foyers (...) de ces surfaces sont dans chaque cas les points stigmatiques (PRAT, Opt., 1962, p. 141).
Prononc. : [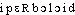]. Étymol. et Hist. 1765 subst. fém. (Encyclop. t. 8); 1830 subst. masc. (CAUCHY, loc. cit.). Formé de hyperbole et de -oïde, v. -ide2.

hyperboloïde [ipɛʀbɔlɔid] adj. et n. m.
ÉTYM. 1765; de hyperbole, et suff. -oïde.
❖
♦ Didactique.
1 Adj. (rare). En forme d'hyperbole.
2 N. m. (1830, Cauchy, in T. L. F.). Math. Quadrique à centre dont les sections planes sont des hyperboles. || Hyperboloïde de révolution : surface engendrée par une hyperbole tournant autour d'un de ses axes.
❖
DÉR. Hyperboloïdal.

Encyclopédie Universelle. 2012.

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Hyperboloide — Hyperboloïde En mathématiques, un hyperboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de posséder un centre de symétrie et de s étendre à l infini. Les… …   Wikipédia en Français

  • Hyperboloide — Hyperboloide, nicht geschlossene Curven 2. Grades, in hyperbolische und elliptische eingetheilt …   Herders Conversations-Lexikon

  • Hyperboloïde — En mathématiques, et plus précisément en géométrie, un hyperboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de posséder un centre de symétrie et de s étendre… …   Wikipédia en Français

  • hyperboloïde — (i pèr bo lo i d ) adj. Terme de géométrie. Qui se rapproche de l hyperbole. Courbes hyperboloïdes.    S. m. Solide produit par la révolution d une hyperbole. ÉTYMOLOGIE    Hyperbole, et terme grec signifiant forme. SUPPLÉMENT AU DICTIONNAIRE… …   Dictionnaire de la Langue Française d'Émile Littré

  • hyperboloïde — hiperboloidas statusas T sritis fizika atitikmenys: angl. hyperboloid vok. Hyperboloid, m rus. гиперболоид, m pranc. hyperboloïde, m …   Fizikos terminų žodynas

  • Hyperboloïde de révolution — ● Hyperboloïde de révolution hyperboloïde engendré par la rotation d une hyperbole autour d un de ses axes de symétrie …   Encyclopédie Universelle

  • Structure hyperboloïde — Sur les autres projets Wikimedia : « Structure hyperboloïde », sur Wikimedia Commons (ressources multimédia) La première structure hyperboloïde au monde la tour de treillage de claire voie d acier située actuellement à Polibino… …   Wikipédia en Français

  • Structures de hyperboloide — Structure hyperboloïde La première structure hyperboloïde par Vladimir Choukhov, Nijni Novgorod, 1896 …   Wikipédia en Français

  • Structures de hyperboloïde — Structure hyperboloïde La première structure hyperboloïde par Vladimir Choukhov, Nijni Novgorod, 1896 …   Wikipédia en Français

  • Modèle de l'hyperboloïde — En géométrie, le modèle de l hyperboloïde, également dénommé modèle de Minkowski ou modèle de Lorentz (d après les noms de Hermann Minkowski et Hendrik Lorentz), est un modèle de géométrie hyperbolique dans un espace de Minkowski de dimension n.… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”